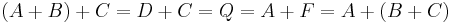Pascal's theorem

In projective geometry, Pascal's theorem (aka Hexagrammum Mysticum Theorem) states that if an arbitrary hexagon is inscribed in any conic section, and pairs of opposite sides are extended until they meet, the three intersection points will lie on a straight line, the Pascal line of that configuration.

Contents

Related results

This theorem is a generalization of Pappus's hexagon theorem – Pappus's theorem is the special case of a degenerate conic of two lines. Pascal's theorem is the polar reciprocal and projective dual of Brianchon's theorem. It was discovered by Blaise Pascal in 1639 when he was 16 years old.

A degenerate case of Pascal's Theorem (four points) is interesting; given points ABCD on a conic Γ, the intersection of alternate sides, AB ∩ CD, BC ∩ DA, together with the intersection of tangents at opposite vertices (A, C) and (B, D) are collinear in four points; the tangents being degenerate 'sides', taken at two possible positions on the 'hexagon' and the corresponding Pascal Line sharing either degenerate intersection. This can be proven independently using a property of pole-polar. If the conic is a circle, then another degenerate case tells us that for a triangle, the three points that appear as the intersection of a side line with the corresponding side line of the Gergonne triangle, are collinear.

Six is the minimum number of points on a conic about which special statements can be made, as five points determine a conic.

The converse is the Braikenridge–Maclaurin theorem, named for 18th century British mathematicians William Braikenridge and Colin Maclaurin (Mills 1984), which states that if the 3 intersection points of the lines through three sides of a hexagon lie on a line, then the 6 vertices of the hexagon lie on a conic; the conic may be degenerate, as in Pappus's theorem. (Coxeter & Greitzer 1967, p. 76) The Braikenridge–Maclaurin theorem may be applied in the Braikenridge–Maclaurin construction, which is a synthetic construction of the conic defined by five points, by varying the sixth point.

The theorem was generalized by Möbius in 1847, as follows: suppose a polygon with 4n + 2 sides is inscribed in a conic section, and opposite pairs of sides are extended until they meet in 2n + 1 points. Then if 2n of those points lie on a common line, the last point will be on that line, too.

If six unordered points are given on a conic section, they can be connected into a hexagon in 60 different ways, resulting in 60 different instances of Pascal's theorem and 60 different Pascal lines. As Thomas Kirkman proved in 1849, these 60 lines can be associated with 60 points in such a way that each point is on three lines and each line contains three points, forming a projective configuration. The 60 points formed in this way are now known as the Kirkman points (Biggs 1981).

Proofs

Pascal's own proof of the theorem has been lost, but there are various proofs for the theorem.

It is sufficient to prove the theorem when the conic is a circle, because any (non-degenerate) conic can be reduced to a circle by a projective transformation; degenerate conics follow by continuity (the theorem is true for non-degenerate conics, and thus holds in the limit of degenerate conic).

A short elementary proof of Pascal's theorem in the case of a circle was found by van Yzeren (1993), based on the proof in (Guggenheimer 1967). This proof proves the theorem for circle and then generalizes it to conics.

We can infer the proof from existence of isogonal conjugate too. If we are to show that X = AB ∩ DE, Y = BC ∩ EF, Z = CD ∩ FA are collinear for conconical ABCDEF, then notice that ADY and CYF are similar, and that X and Z will correspond to the isogonal conjugate if we overlap the similar triangles. This means that angle DYX = angle CYZ, hence making XYZ collinear.

A short proof can be constructed using cross-ratio preservation. Projecting tetrad ABCE from D onto line AB, we obtain tetrad ABPX, and projecting tetrad ABCE from F onto line BC, we obtain tetrad QBCY. This therefore means that R(AB; PX) = R(QB; CY), where one of the points in the two tetrads overlap, hence meaning that other lines connecting the other three pairs must coincide to preserve cross ratio. Therefore XYZ are collinear.

Another proof for Pascal's theorem for a circle uses Menelaus' theorem repeatedly.

Dandelin, the geometer who discovered the celebrated Dandelin spheres, came up with a beautiful proof using "3D lifting" technique that is analogous to the 3D proof of Desargues' theorem. The proof makes use of the property that for every conic section we can find a one-sheet hyperboloid which passes through the conic. Also there exist a simple proof for Pascal's theorem for a circle uses Law of Sines and similarity.

Proof using cubic curves

Pascal's theorem has a short proof using the Cayley–Bacharach theorem that given any 8 points in general position, there is a unique ninth point such that all cubics through the first 8 also pass through the ninth point. In particular if 2 general cubics intersect in 8 points then any other cubic through the same 8 points meets the ninth point of intersection of the first two cubics. Pascal's theorem follows by taking the 8 points as the 6 points on the hexagon and two of the points (say, M and N in the figure) on the would-be Pascal line, and the ninth point as the third point (P in the figure). The first two cubics are two sets of 3 lines through the 6 points on the hexagon (for instance, the set AB, CD, EF, and the set BC, DE, FA), and the third cubic is the union of the conic and the line MN. Here the "ninth intersection" P cannot lie on the conic by genericity, and hence it lies on MN.

The Cayley–Bacharach theorem is also used to prove that the group operation on cubic elliptic curves is associative. The same group operation can be applied on a cone if we choose a point E on the cone and a line MP in the plane. The sum of A and B is obtained by first finding the intersection point of line AB with MP, which is M. Next A and B add up to the second intersection point of the cone with line EM, which is D. Thus if Q is the second intersection point of the cone with line EN, then

(A %2B B) %2B C = D %2B C = Q = A %2B F = A %2B (B %2B C)

Thus the group operation is associative. On the other hand, Pascal's theorem follows from the above associativity formula, and thus from the associativity of the group operation of elliptic curves by way of continuity.

Proof using Bézout's theorem

Suppose f is the cubic polynomial vanishing on the three lines through AB, CD, EF and g is the cubic vanishing on the other three lines BC, DE, FA. Pick a generic point P on the conic and choose λ so that the cubic h = f + λg vanishes on P. Then h = 0 is a cubic that has 7 points A, B, C, D, E, F, P in common with the conic. But by Bézout's theorem a cubic and a conic have at most 3 × 2 = 6 points in common, unless they have a common component. So the cubic h = 0 has a component in common with the conic which must be the conic itself, so h = 0 is the union of the conic and a line. It is now easy to check that this line is the Pascal line.

References

External links

See also